Abstract
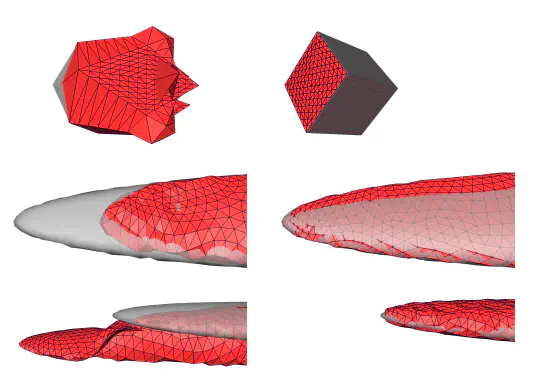
Deformable surface models are often represented as triangular meshes in image segmentation applications. For a fast and easily regularized deformation onto the target object boundary, the vertices of the mesh are commonly moved along line segments (typically surface normals). However, in case of high mesh curvature, these lines may not intersect with the target boundary at all. Consequently, certain deformations cannot be achieved. We propose omnidirectional displacements for deformable surfaces (ODDS) to overcome this limitation. ODDS allow each vertex to move not only along a line segment but within the volumetric inside of a surrounding sphere, and achieve globally optimal deformations subject to local regularization constraints. However, allowing a ball-shaped instead of a linear range of motion per vertex significantly increases runtime and memory. To alleviate this drawback, we propose a hybrid approach, fastODDS, with improved runtime and reduced memory requirements. Furthermore, fastODDS can also cope with simultaneous segmentation of multiple objects. We show the theoretical benefits of ODDS with experiments on synthetic data, and evaluate ODDS and fastODDS quantitatively on clinical image data of the mandible and the hip bones. There, we assess both the global segmentation accuracy as well as local accuracy in high curvature regions, such as the tip-shaped mandibular coronoid processes and the ridge-shaped acetabular rims of the hip bones.
Hans Lamecker
Managing Director
Advancing 3D analysis, planning, design and manufacturing using innovative computational methods and tools